はじめに
三角関数、特に、 \( \sin \) 関数と \( \cos \) 関数はマクローリン展開(テイラー展開)を使って表すことができる。マクローリン展開は無限級数であるため、計算機で求めるときには有限の項に打ち切って求めることになる。では、何次の項まで求めればよいか?
この記事では \( [0, \frac{\pi}{4}] \) の範囲における \( \sin \) 関数と \( \cos \) 関数の値をマクローリン展開を使って求める方法を示す。このとき、double型(64bit浮動小数点型)で十分な精度を達成するための次数(項数)も示す。
結論
結論から言うと、double型で十分な精度を達成するには \( \sin \) 関数は15次まで、\( \cos \) 関数は16次まで求める必要がある。
マクローリン展開による計算方法
三角関数のマクローリン展開は以下のように表すことができる。最後の項は剰余項であり、展開を有限項で打ち切った場合の真の値と展開式との誤差を表す。剰余項の \( \theta \) は \( 0 \lt \theta \lt 1 \) の値で、\( x \) ごとに値が定まる。
\[ \sin(x) = x – \frac{x^3}{3!} + \frac{x^5}{5!} + … + (-1)^{n-1} \frac{x^{2n-1}}{(2n-1)!} + (-1)^n \frac{\cos(\theta x)}{(2n+1)!} x^{2n+1} \tag{1} \]
\[ \cos(x) = 1 – \frac{x^2}{2!} + \frac{x^4}{4!} + … + (-1)^{n-1} \frac{x^{2n-2}}{(2n-2)!} + (-1)^n \frac{\cos(\theta x)}{(2n)!} x^{2n} \tag{2} \]
この展開式を使うことで \( \sin \) や \( \cos \) の値を求めることができる。理論的には無限個の項の和を求めることでどんな x に対しても \( \sin(x) \) や \( \cos(x) \) の値を正確に求めることができる。しかしこの展開式は、 \( x = 0 \) から離れるに従い誤差が大きくなる。
幸い、三角関数には周期性がある。また、\( \sin(\frac{\pi}{2} – x) = \cos(x) \) となる。そのため、適切な変数変換を行うことにより \( x \in [0, \frac{\pi}{4}] \) の場合に帰着できる。
どこまで求めるのか?
以上のことは、適当にWebで検索すればわかることである。では、何項まで計算すれば「十分」と言えるのだろうか?\( sin(x) \approx x \) で求めた場合と同様に剰余項で誤差を評価する。誤差は浮動小数点表記の最後の桁 ulp (unit in the last place) から評価する。
ここでは64bit浮動小数点フォーマット、いわゆるdouble型を考える。ある値 \( z \) を浮動小数点歩表記 \( \tilde{z} = d.dd…dd \times 2^E \) で表した場合、ulpにおける誤差は以下の通りとなる。
\[ E_{ulp} = |z \times 2^{-E} – d.dd…d | \times 2^{52} = |z – \tilde{z} | \times 2^{-E} 2^{52} \]
sin関数の場合
\( \sin(x) \) のマクローリン展開を第 \( n \) 項、\( 2n-1\) 次まで計算した結果を \( S_{2n-1}(x) \) とし、この値と真の値との誤差で ulp を評価した結果は以下の通りとなる。ここで \( E \) は \( \sin(x) \) の値の指数部である。
\[ E_{ulp} = | \sin(x) – S_{2n-1}(x) | \times 2^{-E} 2^{52} \]
この時の剰余項を \( RS_{2n+1}(x) \) とすると (1) のとおり以下のようになる。
\[ \sin(x) – S_{2n-1}(x) = RS_{2n+1}(x) = (-1)^n \frac{\cos(\theta x)}{(2n+1)!} x^{2n+1} \]
この絶対値を上から評価すると以下のようになる。
\[ | RS_{2n+1}(x) | = \left| (-1)^n \frac{\cos(\theta x)}{(2n+1)!} x^{2n+1} \right| = \frac{\cos(\theta x)}{(2n+1)!} x^{2n+1} \le \frac{x^{2n+1}}{(2n+1)!} \]
\( \cos (\theta x) \) の評価は \( x \in [0, \frac{\pi}{4}] \) を仮定した。以上より、ulpにおける誤差 \( E_{ulp} \) および、\( E_{ulp} \) を上から評価した \( E_{ulp}^+ \) は以下のようになる。
\[ E_{ulp} = |RS_{2n+1}(x)| \times 2^{-E} 2^{52} \]
\[ E_{ulp}^+ = \frac{x^{2n+1}}{(2n+1)!} \times 2^{-E} 2^{52} \]
\( x \) が減少すると \( E_{ulp}^+(x) \) の \( x^{2n+1} \) は急激に小さくなる。一方、\( E \) は \( \sin(x) \) の指数部であるため \( 2^{-E} \) は増加する。イメージとしては以下の図のようになる。\( x = \frac{\pi}{4} \) から値を小さくすると\( E_{ulp}^+(x) \) は減少する。この時、\( \sin(x) \ge 1/2 \) だから \( E = -1 \) である。そして、\( x \) が \( \frac{\pi}{6} \) を超えて小さくなるとき、\( E = -2 \) になるため ULP での誤差が倍に上昇する。
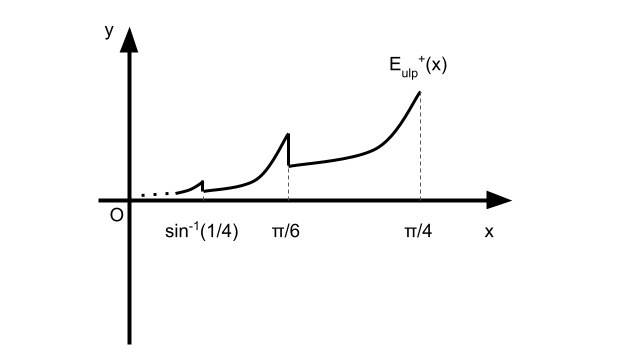
\( x \) の減少に対して減少する部分と増加する部分があるが、\( E_{ulp}^+(x) \) では全体としては減少する部分の寄与が大きい。これはのちの記事で示す予定である。したがって、\( [0, \frac{\pi}{4}] \) の範囲で \( E_{ulp}^+(x) \) が最大となるのは \( x = \frac{\pi}{4} \) の時である。
ulpが最大になるところで0.5を下回っていれば十分な精度が出ているとみなしてよい。これまでの議論で \( x = \frac{\pi}{4} \) の時に最大になるから、この時の \( E_{ulp}^+(x) \) が0.5を下回るような \( n \) を探すと \( n=8 \) の時となる。つまり、展開式としては \( 2n-1 = 15\) 次まで求めればよいことになる。
| n | \( E_{ulp}^+ \) |
| 1 | 727290917205962 |
| 2 | 22431480116651 |
| 3 | 329449159051 |
| 4 | 2822511172 |
| 5 | 15827879.93 |
| 6 | 62586.10315 |
| 7 | 183.8393093 |
| 8 | 0.4169166488 |
cos関数の場合
\( \cos \) 関数の場合も \( \sin \) 関数と同様に項数を決めていく。
\( \cos(x) \) のマクローリン展開を第 \( n \) 項、\( 2n-2\) 次まで計算した結果を \( C_{2n-2}(x) \) とし、この値と真の値との誤差で ulp を評価した結果は以下の通りとなる。ここで \( E \) は \( \cos(x) \) の値の指数部である。
\[ E_{ulp} = | \cos(x) – C_{2n-2}(x) | \times 2^{-E} 2^{52} \]
この時の剰余項を \( RC_{2n}(x) \) とすると (2) のとおり以下のようになる。
\[ \cos(x) – C_{2n-2}(x) = RC_{2n}(x) = (-1)^n \frac{\cos(\theta x)}{(2n)!} x^{2n} \]
この絶対値を上から評価すると以下のようになる。
\[ | RC_{2n}(x) | = \left| (-1)^n \frac{\cos(\theta x)}{(2n)!} x^{2n} \right| = \frac{\cos(\theta x)}{(2n)!} x^{2n} \le \frac{x^{2n}}{(2n)!} \]
\( \cos (\theta x) \) の評価は \( x \in [0, \frac{\pi}{4}] \) を仮定した。以上より、ulpにおける誤差 \( E_{ulp} \) および、\( E_{ulp} \) を上から評価した \( E_{ulp}^+ \) は以下のようになる。
\[ E_{ulp} = |RC_{2n}(x)| \times 2^{-E} 2^{52} \]
\[ E_{ulp}^+ = \frac{x^{2n}}{(2n)!} \times 2^{-E} 2^{52} \]
\( x \) が減少すると \( E_{ulp}^+(x) \) の \( x^{2n} \) は急激に小さくなる。\( \sin(x) \) の時とは異なり、\( x \in [0, \frac{\pi}{4}] \) の間は \( \cos(x) \)の指数部は -1のままである。したがって、\( 2^{-E} \) の部分は変化せず 2 のままになる。イメージは以下の図のようになる。
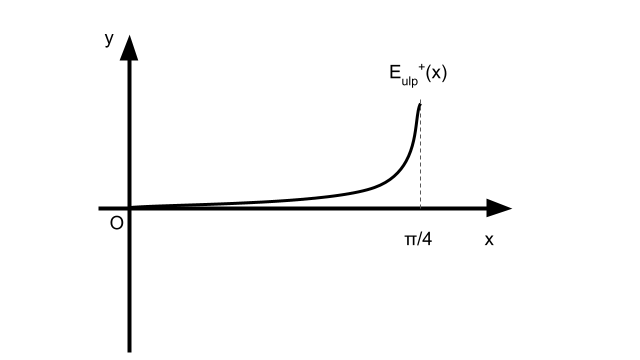
したがって、\( [0, \frac{\pi}{4}] \) の範囲で \( E_{ulp}^+(x) \) が最大となるのは \( x = \frac{\pi}{4} \) の時である。
\(\sin\)関数の時と同様に考えて、ulpが最大になるところで0.5を下回っていれば十分な精度が出ているとみなしてよい。これまでの議論で \( x = \frac{\pi}{4} \) の時に最大になるから、この時の \( E_{ulp}^+(x) \) が0.5を下回るような \( n \) を探すと \( n=9 \) の時となる。つまり、展開式としては \( 2n-2 = 16\) 次まで求めればよいことになる。
| n | \( E_{ulp}^+ \) |
| 1 | 2.77805E+15 |
| 2 | 142803237657302 |
| 3 | 2936273880984 |
| 4 | 32343595556 |
| 5 | 221679509.1 |
| 6 | 1035932.319 |
| 7 | 3511.072176 |
| 8 | 9.024190991 |
| 9 | 0.01819142057 |
コメント