本節では三角関数 \( \sin \) 、 \( \cos \) とそのマクローリン展開との差が単調増加もしくは単調減少することを示す。
例えば、\( \sin(x) \) と展開式の1項目 \( x \) との差について考える。この差についての導関数を求めると \( (\sin(x) – x)’ = \cos(x) – 1 \le 0\) となる。\( x \) が0から正の方向に進む場合、単調減少となり、\( \sin(x) \) に比べて \( x \) が単調に増加する。つまり、差が開く。一方、\( x \) が0から負の方向に進む場合、負の方向に単調増加となり、\( \sin(x) \) に比べて \( x \) が単調に増加する。この場合も差が開く。
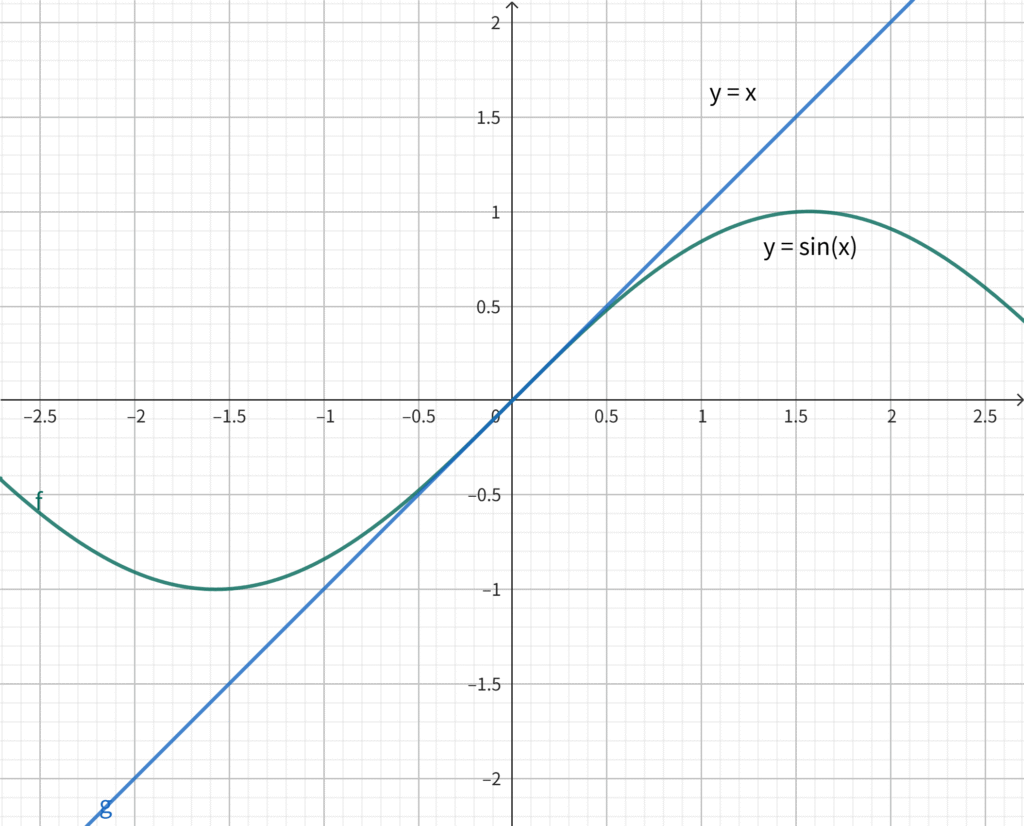
\( \sin(x) \) と \( x \) の差について示したが、任意の項数のマクローリン展開式との差でも同様の性質が得られる。また、\( \cos(x) \) と2以上の任意の項数のマクローリン展開式でも同様である。
三角関数のマクローリン展開
三角関数のマクローリン展開は以下のように表すことができる。最後の項は剰余項であり、展開を有限項で打ち切った場合の真の値と展開式との誤差を表す。剰余項の \( \theta \) は \( 0 \le \theta \le 1 \) の値で、\( x \) ごとに値が定まる。
\[ \sin(x) = x – \frac{x^3}{3!} + \frac{x^5}{5!} + … + (-1)^{n-1} \frac{x^{2n-1}}{(2n-1)!} + (-1)^n \frac{\cos(\theta x)}{(2n+1)!} x^{2n+1} \tag{1} \]
\[ \cos(x) = 1 – \frac{x^2}{2!} + \frac{x^4}{4!} + … + (-1)^{n-1} \frac{x^{2n-2}}{(2n-2)!} + (-1)^n \frac{\cos(\theta x)}{(2n)!} x^{2n} \tag{2} \]
展開式というときは上記の式から剰余項を除いたものとなる。以降、\( \sin \) 関数の \( 2n-1 \) 次までの展開式を \( S_{2n-1}\)、 \( \cos \) 関数の \( 2n-2 \) 次までの展開式を \( C_{2n-2}\) とする。これらの展開式は \( x = 0 \) のとき、\( \sin(x) \) または \( \cos(x) \) に一致する。
\[ S_{2n-1}(x) = \sum_{k=1}^{n} (-1)^{k-1} \frac{x^{2k-1}}{(2k-1)!} \]
\[ C_{2n-2}(x) = \sum_{k=1}^{n} (-1)^{k-1} \frac{x^{2k-2}}{(2k-2)!} \]
展開式の微分
関数の差が単調に増大することを示すのに導関数を求める必要があるため、展開式の微分を計算しておく。\( S_{2n-1}\) と\( C_{2n-2}\) の微分は以下のようになり、\( \sin \) 関数と \( \cos \) 関数に似た関係式が得られる。
\begin{eqnarray}
S_{2n-1}'(x) &=& \sum_{k=1}^{n} (-1)^{k-1} \frac{(2k-1)}{(2k-1)!}x^{2k-2} \\
&=& \sum_{k=1}^{n} (-1)^{k-1} \frac{x^{2k-2}}{(2k-2)!} \\
&=& C_{2n-2}(x)
\end{eqnarray}
\begin{eqnarray}
C_{2n-2}'(x) &=& \sum_{k=2}^{n} (-1)^{k-1} \frac{(2k-2)}{(2k-2)!}x^{2k-3} \\
&=& \sum_{k=2}^{n} (-1)^{k-1} \frac{x^{2k-3}}{(2k-3)!}
\end{eqnarray}
ここで、 \( k = k’+1 \) となるように変数を変換をすると以下のようになる。
\begin{eqnarray}
C_{2(n-1)}'(x) &=& \sum_{k’=1}^{n-1} (-1)^{k’} \frac{x^{2k’-1}}{(2k’-1)!} \\
&=& -\sum_{k’=1}^{n-1} (-1)^{k’-1} \frac{x^{2k’-1}}{(2k’-1)!} \\
&=& -S_{2(n-1)-1}
\end{eqnarray}
関数の差が増大する条件
関数 \( f(x) \) と \( g(x) \) が \( x = 0 \) で等しいとする。この2つの関数が \( x = 0 \) から離れるにつれ、その差の絶対値が増大することを示すには何を示せばよいか?いわゆる、十分条件を求めていく。
\( (f(x) – g(x))^2 \) が \( x > 0 \) で単調増加、\( x < 0 \) で単調減少することを示せばよい。\( D(x) = f(x) – g(x) \) とし、この関数の2乗の微分を求めると以下のようになる。
\[ (D(x)^2)’ = 2 D(x) D'(x) \]
\( x > 0 \) の時には \( (D(x)^2)’ = 2 D(x) D'(x) > 0 \) になっていなければならない。\( D(0) = 0 \) なので、もし \( D'(x) \) が \( x > 0 \) の範囲で常に正であれば \( D(x) \) も正になる。(これは平均値の定理より示せる。)ゆえに、条件を満たす。同様に、\( D'(x) \) が常に負であれば \( D(x) \) も負になり、この時も条件を満たす。したがって、\( x > 0 \) の範囲で \( D'(x) \) の符号が変わらなければ条件を満たすと言える。
\( x < 0 \) の時には \( (D(x)^2)’ = 2 D(x) D'(x) < 0 \) になっていなければならない。\( D(0) = 0 \) なので、もし \( D'(x) \) が \( x < 0 \) の範囲で常に負であれば \( D(x) \) は正になり、条件を満たす。同様に、\( D'(x) \) が常に正であれば \( D(x) \) は負になり、この時も条件を満たす。したがって、\( x < 0 \) の範囲で \( D'(x) \) の符号が変わらなければ条件を満たすと言える。
以上をまとめると、\( x > 0 \) と \( x < 0 \) のそれぞれの領域で、\( D'(x) \) すなわち、\( f'(x) – g'(x) \) の符号が変わらないことを示せば十分である。
展開式との差
\( \sin \) 関数、 \( \cos \) 関数とそのマクローリン展開式 \( S_{2n-1} \)、 \( C_{2n} \)との差は \( x \) が0から離れると大きくなることを \( n \) に対する帰納法で証明する。
実は、\( \cos \) 関数と \( C_0 \) との差は単調に増加しない。単調に増加するのは \( C_2 \) からである。
基底段階 (n=1 の場合)
\( \sin \) 関数と展開式 \( S_{2n-1} \) の差は以下のとおりである。
\[ \sin(x) – S_{2n-1}(x) = \sin(x) – S_{1}(x) = \sin(x) – x \]
この導関数は以下のように評価でき、常に負である。
\[ (\sin(x) – x)’ = \cos(x) – 1 \le 0 \]
\( x > 0 \)、\( x < 0 \) のそれぞれの領域で差の導関数の符号が変化しない。そのため、\( \sin(x) – x \) の絶対値は \( x \) が0から離れるにつれて単調に増加する。また、符号もそれぞれの領域で変化しない。
\( \cos \) 関数と展開式 \( C_{2n} \) の差は以下のとおりである。
\[ \cos(x) – C_{2n}(x) = \cos(x) – C_{2}(x) = \cos(x) – \left(1 – \frac{x^2}{2!} \right) \]
この導関数は以下のように評価できる。
\[ \left(\cos(x) – \left(1 – \frac{x^2}{2!} \right) \right)’ = -(\sin(x) – x) \]
\( \sin(x) – x \) の符号が \( x > 0 \)、\( x < 0 \) のそれぞれの領域で変化しないことはすでに示したとおりである。したがって \( \cos(x) – \frac{x^2}{2!} \) の絶対値は \( x \) が0から離れるにつれて単調に増加する。また、符号もそれぞれの領域で変化しない。
帰納段階
\( n=k \) のとき、\( \sin(x) = S_{2k-1}(x) \) 、 \(\cos(x) – C_{2k}(x) \) は \(x\) が0から離れるにつれ、絶対値が単調に増加するとする。このとき、 \( x > 0 \) 、\( x < 0 \) のそれぞれの範囲全体で差の符号は変わらない。この仮定の下で \( \sin(x) – S_{2(k+1)-1}(x) \) 、\( \cos(x) – C_{2(k+1)}(x) \) についても同様の性質が言えることを示す。
\( \sin(x) – S_{2(k+1)-1}(x) \) の導関数は先に求めた展開式の微分を用いると以下のとおりになる。
\[ (\sin(x) – S_{2(k+1)-1}(x))’ = \cos(x) – C_{2(k+1)-2}(x) = \cos(x) – C_{2k}(x)\]
帰納法の仮定より、導関数である \( \cos(x) – C_{2k}(x) \) は \( x > 0 \) 、\( x < 0 \) のそれぞれの範囲全体で差の符号は変わらない。したがって、\( \sin(x) – S_{2(k+1)-1}(x) \) は\(x\) が0から離れるにつれ、絶対値が単調に増加することが示せた。
\( \cos(x) – C_{2(k+1)}(x) \) の導関数も同様に先に求めた展開式の微分を用いると以下のとおりになる。
\[ (\cos(x) – C_{2(k+1)}(x))’ = -\sin(x) + S_{2(k+1)-1} = -(\sin(x) – S_{2(k+1)-1})\]
直前の議論より、\( \sin(x) – S_{2(k+1)-1} \) は \( x > 0 \) 、\( x < 0 \) のそれぞれの範囲全体で差の符号は変わらない。したがって、\( \cos(x) – C_{2(k+1)}(x) \) は\(x\) が0から離れるにつれ、絶対値が単調に増加することが示せた。
以上の議論より、\( \sin \) 関数、 \( \cos \) 関数とそのマクローリン展開式 \( S_{2n-1} \)、 \( C_{2n} \)との差は \( x \) が0から離れると大きくなることが示せた。

コメント