三角関数の値の求め方

人類社会における三角関数の必要性については今更議論の余地もないだろう。問題は、どのようにしてその値を求めるかである。

Linuxではsin関数をはじめとした数学関数はglibcライブラリで実装されている。実際に以下のコードをデバッガ (gdb) で実行することでsysdeps/ieee754/dbl-64/s_sin.cへの参照が確認できる。

#include <math.h>
#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{
    double x, y;
    if (argc > 1) {
        x = atof(argv[1]);
    } else {
        x = 1.0f;
    }
    y = sin(x);
    printf("sin(%f) = %f\n", x, y);

    return 0;
}

(gdb) b sin
Breakpoint 1 at 0x1090
(gdb) r
Starting program: /home/misuzu/analyze_sin/a.out 

Breakpoint 1, __sin_fma (x=1) at ../sysdeps/ieee754/dbl-64/s_sin.c:202
202	../sysdeps/ieee754/dbl-64/s_sin.c: No such file or directory.

該当のコードはglibcのgitリポジトリから参照できる。大きさが523MBもあるクソデカリポジトリなので注意。

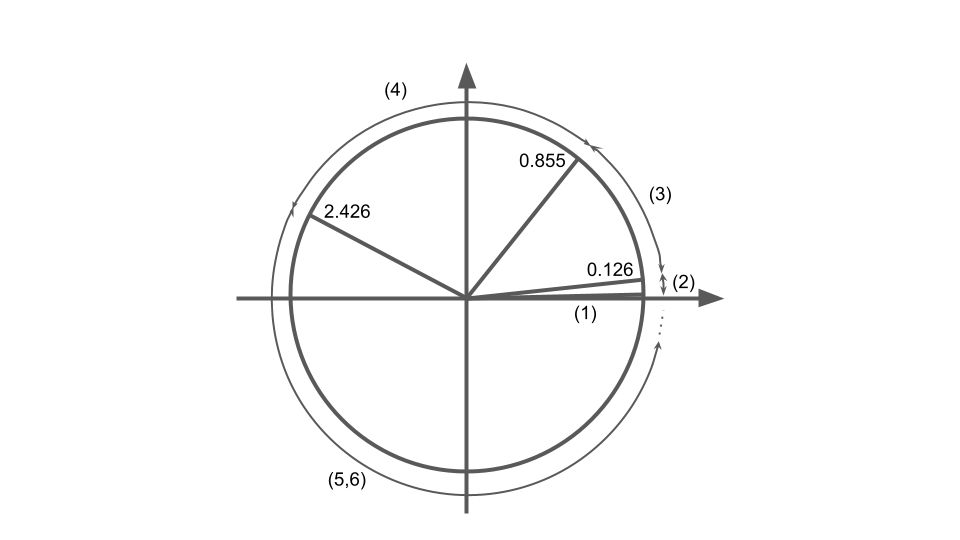
sourceware.org Git - glibc.git/blob - sysdeps/ieee754/dbl-64/s_sin.c

この実装ではsin関数は以下の6パターンで処理を変えている。

$ |x| < 2^{-26} $ の場合
$2^{-26} \le |x| < 0.126$ (大体7.2°) の場合
$0.126 \le |x| < 0.855469$ (大体49°) の場合
$0.855469 \le |x| < 2.426265$ (大体140°) の場合
$2.426265 \le |x| < 105414350$ の場合
$105414350 \le |x| < 2^{1024}$ の場合

$ |x| < 2^{-26} $ の場合

入力が極めて小さい場合は以下のように近似し、入力値をそのまま返す。

$$ \sin(x) \approx x$$

$2^{-26} \le |x| < 0.126$ (大体7.2°) の場合

$|x| < 0.126$ (大体7.2°) の時はマクローリン展開によりsin(x) の値を求める。基本的には定義どおりのマクローリン展開だが、次数が高くなるに連れて実際の係数と値が変わってくる。おそらく、チェビシェフ補間の式が混ざっていると思われる（要確認）。

$0.126 \le |x| < 0.855469$ (大体49°) の場合

$0.126 \le |x| < 0.855469$ (大体49°) の場合はテイラー展開とsin, cosのテーブル参照で計算する。最終的にこれらの値を加法定理で組み合わせて出力する。

$0.855469 \le |x| < 2.426265$ (大体140°) の場合

$|x| < 2.426265$, (大体140°) の範囲にある場合はcosの計算に帰着してsin(x)の値を求めている。

xが十分大きい場合、極めて大きい場合

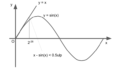
$|x| \ge 2.426265$, (大体140°) を超える場合、Range reductionと呼ばれる処理が必要になる。三角関数は周期関数であり、符号や周期に対して対称である。例えば、以下のようにsin関数は$2\pi$の周期を持ち、0で反転する。また、$\pi / 2$で対称になる。

$$\sin(x) = -\sin(-x) = -\sin(2\pi – x) = \sin(2\pi + x)$$

$$\sin(\pi / 2 – x) = \sin(\pi / 2 + x)$$

したがって、$|x|$が大きな値の場合、上記の性質を使用して $|x| < \pi/4$ になるように変換し、その値からsin(x)の値を求めていくことになる

三角関数の値の求め方

\( |x| < 2^{-26} \) の場合

\(2^{-26} \le |x| < 0.126\) (大体7.2°) の場合

\(0.126 \le |x| < 0.855469\) (大体49°) の場合

\(0.855469 \le |x| < 2.426265\) (大体140°) の場合

xが十分大きい場合、極めて大きい場合

コメント