はじめに
以前の記事ではglibcにおける三角関数の計算方法を紹介した。そして、\(|x|\) が極めて小さい場合、\(\sin(x) \approx x\) と近似して出力していることも述べた。では、どのくらいの値であればこの様に近似できるのか?この記事ではそれを評価する。
そもそも「\(\sin(x) \approx x\) と近似してよい」、とはどういうことか?それは \(\sin(x)\) と \( x \) のそれぞれの浮動小数点表記が一致するということである。より厳密に言うと、浮動小数点表記の「最後の桁で規格化した誤差」が0.5以下であることを求めている。この「最後の桁で規格化した」という表現を ulp (at the unit of the last place) と呼ぶ。
例えば、円周率は \(\pi = 3.14159265359 … \) という実数であり、無限小数である。これを3.14と表現したとき、誤差は \(0.00159265359… \) となる。そして、この誤差を最後の桁 (0.01) で規格化した数字が \(0.159265359…\) である。ulpが0.5以下になるということは、「最後の桁までは合っている」ということを意味する。
したがって、\(\sin(x)\) と \( x \) のulpでの誤差が0.5以下になる \( x \) の範囲を求めることが本記事の内容である。
ulpの定義
ulpの計算方法に関してはこのサイトが詳しい。元々Sun Microsystemsの技術者が著した文献であり、現在はOracleのサイトから参照できる。
ある実数 \(z\) を仮数部の桁数がp、指数部の値がeである浮動小数点数 \( \tilde{z} = d.dd…d \times 2^e \) で表現したときのulpは以下のように表すことができる。
$$ ulp = |z \times 2^{-e} – d.dd…d | \times 2^{p-1} = |z – \tilde{z} | \times 2^{-e} 2^{p-1} $$
計算機でよく使われる64bit浮動小数点フォーマットの場合、仮数部の桁数は暗黙の1を含んで53桁である。したがって、ulpは次のように表される。
$$ ulp = |z \times 2^{-e} – d.dd…d | \times 2^{52} = |z – \tilde{z} | \times 2^{-e} 2^{52} \tag{1}$$
\(\sin(x) \approx x\) としたときの誤差
\(\sin(x) \approx x\) としたときの誤差は、\(\sin(x) \) のマクローリン展開を1次で打ち切ったときの展開式から得られる。
$$ \sin(x) = x – \frac{\cos (\theta x)}{3!} x^3$$
ここで \(\theta\)は \(0 < \theta < 1\) の数である。ここから \( | \sin(x) – x | \) を評価する。
$$ | \sin(x) – x | = | – \frac{\cos (\theta x)}{3!} x^3 | \le \frac{1}{6} | x^3 | =\frac{1}{6} | x |^3 \tag{2} $$
最後の不等式は \( -1 \le \cos (\theta x) \le 1 \) であることを使用した。実際、\(x\) は極めて小さいため、\( | \cos (\theta x) | \) はほとんど1である。次に、\(x\) を浮動小数点表現 \(\tilde{x} \) で表現し、その時の仮数部、指数部をそれぞれ \(M, E\) とすると、\( \tilde{x}\) は次のように表記される。
$$ |\tilde{x}| = M \times 2^E $$
ここで、仮数部の\(M\)は \( 1 \le M < 2 \) を満たすため、\(|\tilde{x}|\)の範囲は以下のようになる。
$$ 2^E \le |\tilde{x}| = M \times 2^E < 2^{E+1} \tag{3} $$
これをulpの定義式 (1) 、 \(| \sin(x) – x |\) の不等式 (2)、\(|\tilde{x}|\)の不等式 (3) を適用すると以下のようにulpを上から押さえることができる。
$$ ulp = |\sin(\tilde{x}) – \tilde{x} | 2^{-E} 2^{52} \le \frac{1}{6} | \tilde{x} |^3 2^{-E} 2^{52} < \frac{1}{6} 2^{2E + 55} $$
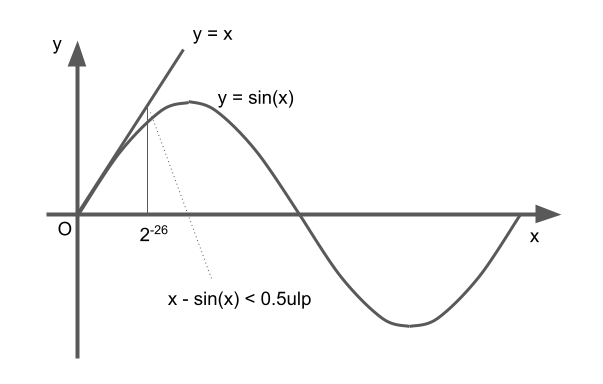
\( \frac{1}{6} 2^{2E + 55} \le 0.5 \) となるEを求めると \( E < -26 \) となる。これは「 \(|x|<2^{−26} \) の場合」という条件式に当てはまる。



コメント