 math
math 三角関数の値の求め方(マクローリン展開)
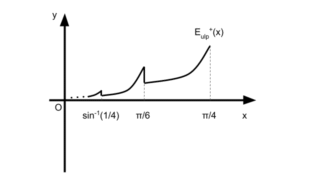
この記事では三角関数、特に、 \( \sin \) 関数と \( \cos \) 関数を\( [0, \frac{\pi}{4}] \) の範囲でマクローリン展開(テイラー展開)を使って求める場合、必要な項数が \( \sin \) 関数では15次まで、\( \cos \) 関数では16次まで求める必要があることを示す。
 math
math 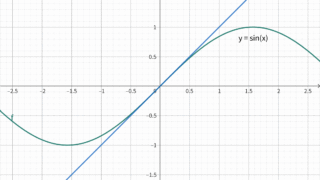 math
math 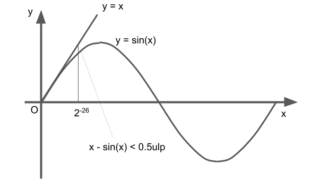 Linux
Linux 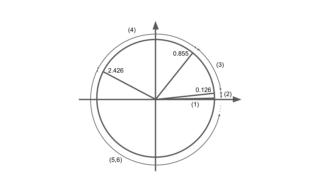 Linux
Linux